- 相関係数(r)の値をそのまま信じてはいけないことがわかる
- ハマりがちな相関の3つの落とし穴が何かわかる
- 落とし穴にハマらないために図を書くことが大事だとわかる

新商品のアイス、売上回復したみたいですね。なぜだと思いますか?



気温と売上の相関係数が0.7で気温の影響によるものだと思います。



引き続きモニターしているのですね



はい!相関は便利ですね。他の商品にも応用できて助かってます



何の商品に応用できたんです?



新製品のチョコです!相関係数は0.6で気温が上がると売上が上がるみたいです



夏場チョコはむしろ売上が下がる傾向があるのですが。相関の落とし穴にハマってませんか?



落とし穴があるんですか



一緒にデータを確認してみましょうか
こんにちは、おちです。2つの間に相関があるかを確認するとき、相関係数だけみてないでしょうか?
実は相関がない場合や別の関係が隠れている場合があります。
今回はハマりがちな相関の3つの落とし穴について解説していきます。
2人の会話のアイスと売上の関係が気になる方はこちらの記事をご覧ください。


ハマりやすい3つの落とし穴


落とし穴①:極端な値に引っ張られている場合がある
極端な値がデータ相関係数を押し上げている場合があります。こんな感じです。


このグラフの相関係数は0.7です。1点だけ極端な点があるせいで右肩上がりの直線が引けてしまいます。右上の極端な値を外したらどうなるでしょう?
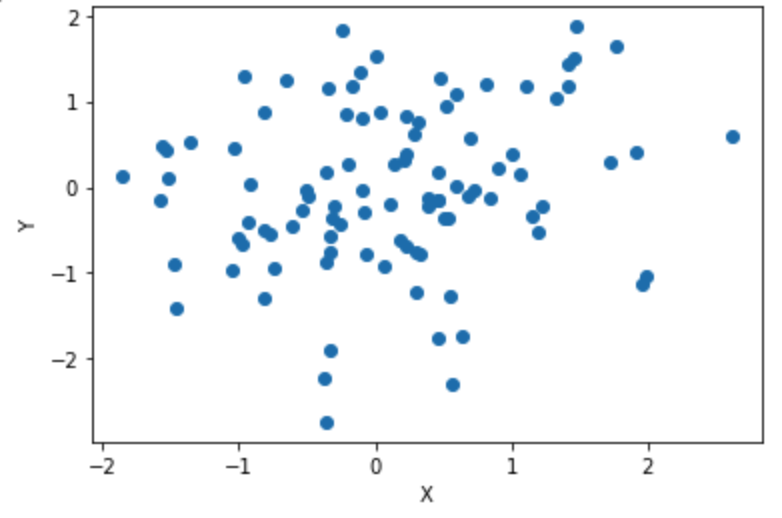

2つの間に比例っぽい関係はなさそうですよね。1点外すだけでこのグラフの相関係数は0.2になります。
グラフを書かずに機械的に表から相関係数を出すとこの落とし穴が待っています。気をつけましょう。
ちなみに極端な値のことを統計学の世界では外れ値と呼びます。
落とし穴②:第3の要因が隠れている場合がある
間に挟まっている要因のせいで2つの間に相関関係があるように見える場合があります。
夏場のアイスの売上と熱中症患者数に正の相関があったとしましょう。


これは気温という第3の要因が隠れていそうですよね。


第3の要因のせいで相関しているように見えるものを擬似相関と呼びます。
扱うデータの背景知識がないと隠れた関係に中々気づけないので注意です。
ビジネスに相関を活かすときは、業界の常識や専門知識とデータをすり合わせて擬似相関ではないか考えると誤った判断を回避できます。
落とし穴③:二次関数のような曲線的な関係な場合がある
実は2つの間に関係はあるけど相関係数上は相関がないという結果になる場合があります。例えば以下のような関係のグラフです。
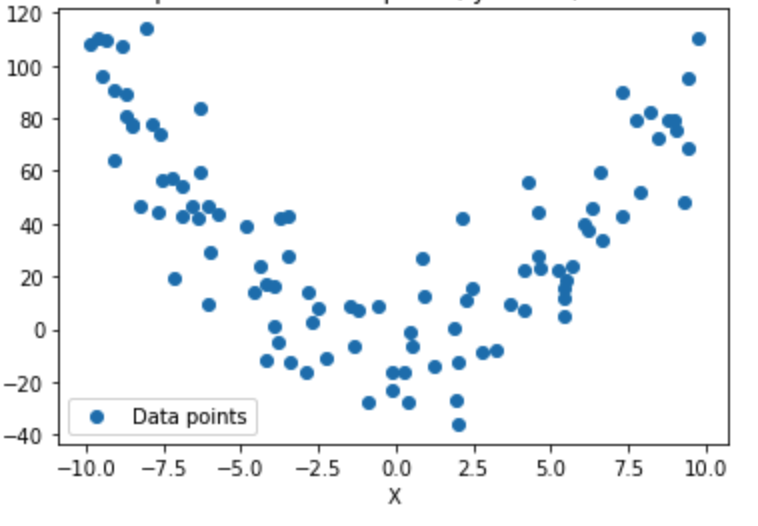

相関係数だけみていると直線以外の関係を見落としてしまいます。
図に書くことで見落としを防げます
今回のビジネス事例の場合
2人が話していたチョコレートの売上と気温(最高気温)の関係を見てみましょう。


どうやら外れ値があるようです。
この外れ値を除いたときのグラフは以下のとおりです。
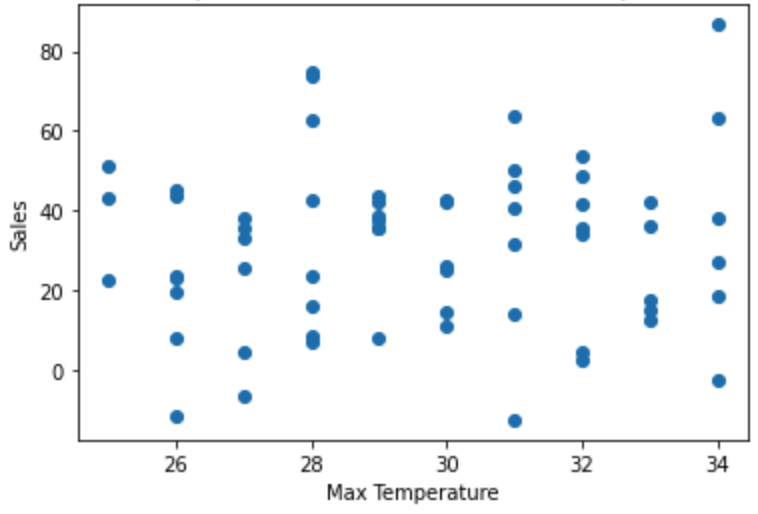

外れ値を除くと特に相関はなさそうです。



ある番組で紹介されて売上が急増した日があるみたいですね



相関に引っ張られず冷静に分析するようにします
まとめ:データを図に書こう!
今回は相関の3つの落とし穴について解説しました。
相関係数の数字だけ見るとデータ同士の関係性を間違ってしまう恐れがあります。
俯瞰して冷静に眺めるために図に書くようにしましょう。
今回は以上です。ありがとうございました。

