こんにちは、おちです。
数式の説明がないシリーズが好評です。ありがとうございます。
引き続き、数式による説明は他のサイトや専門書にお任せして、今回は標準誤差についてご紹介していきます。
 にゃん太
にゃん太標準偏差とはまた別なの?
どちらもばらつきを表していますが、指し示している部分が違います。自分がどの部分のばらつきを見たいかで使い分けます。
標準誤差とは?(数式説明なし)
標準偏差はあるグループ全体のばらつき具合を見る時に便利なのに対して、標準誤差はあるグループの本当の平均値がどの範囲内にいるのか考える時に便利な指標となります。
具体例を示しながら詳細説明していきます。
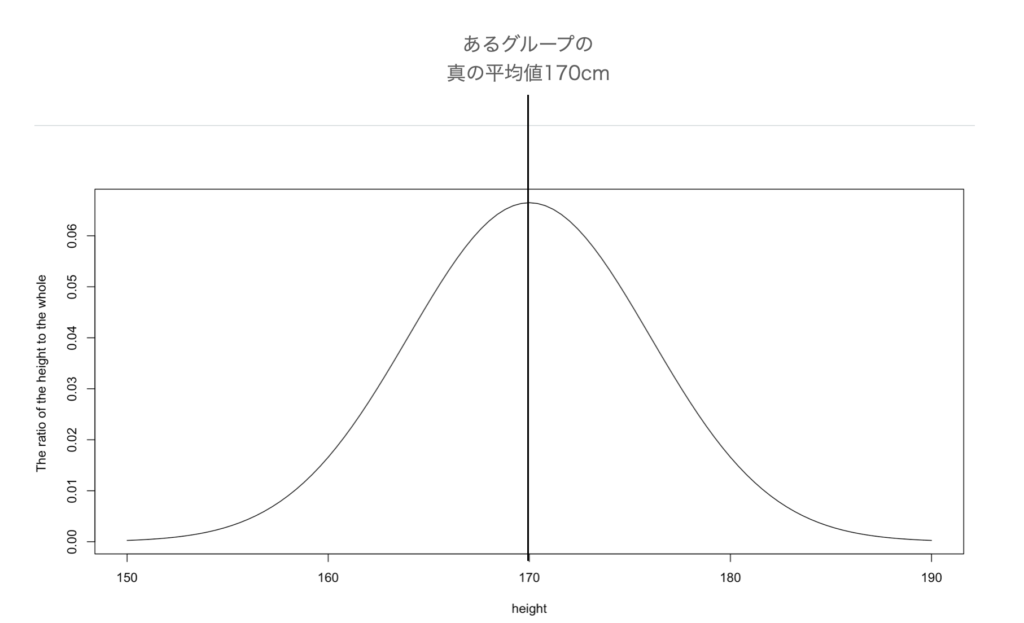

上図は、あるグループ1万人全員の身長の分布を調べた結果だとします。
真の平均値は170.0cmでした。
調べたい対象グループの分布を正確に知りたい場合は全員の身長を調べれば求めることができます。
ただ、1万人の身長を測るには膨大な時間がかかります。
そこで1万人のグループからランダムに10人選び出して、このグループの身長の分布を推測することにしました。
上記のように全数検査に膨大な時間がお金が必要だけど、グループの傾向や特徴を知りたいときに統計を利用すると調べるための時間やお金を節約できて便利です。
10人測定した結果が下になります。


この10人の身長の平均は170.7cm、標準誤差は2.0cmでした。
1万人測定したときの平均値よりも0.7cm高い値が出ました。
このように少ないサンプルであるグループの傾向・特徴をつかもうとすると、真の平均値からブレてしまいます。
このブレの範囲がどれくらいかを示してくれるのが標準誤差です。
10人測定した結果から、1万人のグループの身長の平均は95%の確率で170.7±2.0cmの範囲にいると統計的に言えます。
実際に、真の平均値170.0cmはこの範囲に入っています。
標準誤差のブレ幅を小さくしたいときは測定する数を増やそう
先ほどの結果では170.7±2.0cmの範囲に真の平均値があると求めることができました。
この2cmのブレ幅をもっと小さくしたい場合は測定する数を増やすことでブレ幅を小さくすることができます。
先ほどと同じグループから50人ランダムに選んで身長を測定してみました。


50人の測定結果は平均値171.5cm、標準誤差0.7cmでした。
標準誤差の値はサンプル数が増えれば増えるほど小さくなります。
本当の平均値がいるであろう範囲を小さくしたい時は測定サンプル数を増やすのも一つの手です。
注意点は、測定サンプル数を安易に増やすと必ず標準誤差は小さくなりますし、統計でよく出る有意差というものも出やすくなってしまう点です。
自分が見たいグループの特徴・傾向をどれくらい掴みたいのかを予め考えて、サンプルの数を決めることが重要です。
50人測定した結果が良い(悪い?)例で、95%の確率で171.5±0.7cmの範囲に真の平均値がいると統計的に言えます。
ただ、残念ながら真の平均値170.0cmは今回範囲に入りませんでした。統計的に50人測定を100回やったら5回起こり得る事態が今回起きました。
上記のような場合があることも踏まえて、標準誤差を扱っていただけると嬉しいです。
最後に
今回は標準誤差についてお話ししました。
標準偏差があるグループ全体のばらつきの傾向を示す指標に対して、標準誤差は平均値のブレ幅を示す指標です。
ある2つのグループの平均値に差が出ているかどうかを確かめたい時などにご活用いただけたら嬉しいです。
以上です。最後までお付き合いくださりありがとうございました。

