こんにちは、おちです。
データ分析するときはデータを図に起こすことが大事です。
データを図に起こすことで色々な気づき、示唆を得られることは間違いないです。
ただ、見たいもの全てのデータを手に入れることは現実問題難しいことが多いです。
例えば、工場である製品を大量に作っていると、機械動作のブレや素材のブレによってたまに規格から外れた製品ができてしまうことがあります。
お客様に安定した品質をお届けするためにはこの規格から外れた製品が出てくる頻度を最小に抑える必要があります。
規格外品の発生頻度を求める場合、理想は全数検査ですが検査にかかる労力やお金を考えると中々難しいです。
この時役立つのが統計です。
限られたサンプル数から規格外品の発生率を推測することができます。
今回は限られたサンプルデータから全体像を把握する方法、考え方をご紹介していきます。
平均値、標準偏差を使って全体の傾向を推測しよう
実際に見たいものの全体像を限られたサンプルデータから想像・推測してみましょう。
下の図はクッキーを大量に製造している工場から15個サンプルを抜き取って重量を測定したデータになります。

これを図に起こしてみましょう。
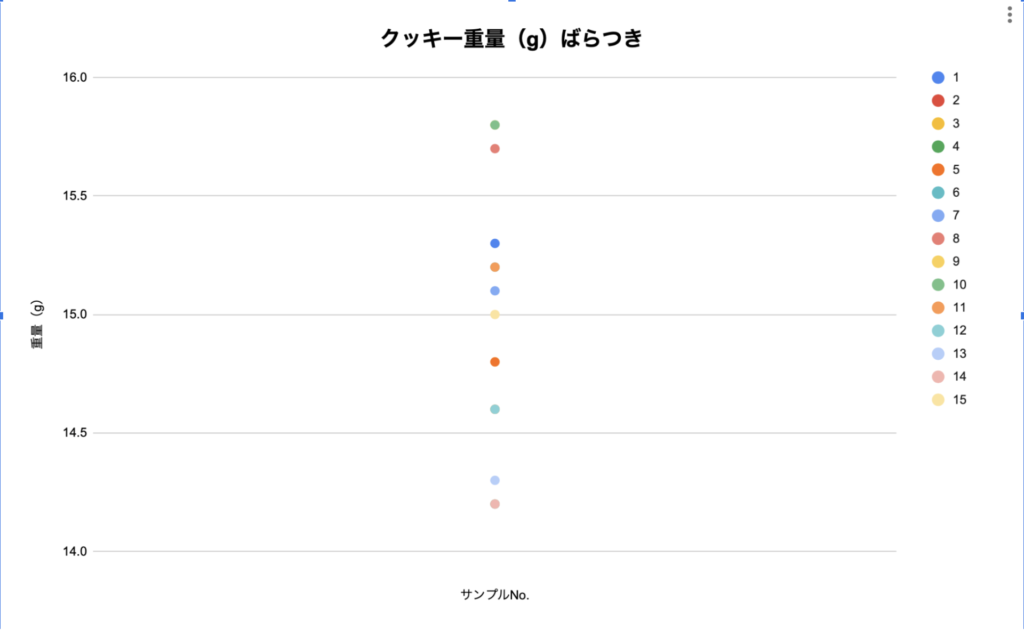
図に起こしてみると、15サンプル中11サンプルは14.5g〜15.5gの範囲に収まっていて、4サンプルがこの範囲から外れてしまっていることが読み取れます。
また、特別飛び抜けて大きすぎたり、小さすぎたりするデータはなさそうで15gくらいで平均値を取りそうな感じがします。
この15個という限られたデータから、大量に製造したクッキー重量の平均値とブレ幅を推測することができます。
そこで登場するのが、別の記事でご紹介した平均値と標準偏差です。
エクセルなどの表計算ソフトでは平均値はAVERAGE関数、標準偏差はSTDEVまたはSTDEV.S関数を使うと求められます。
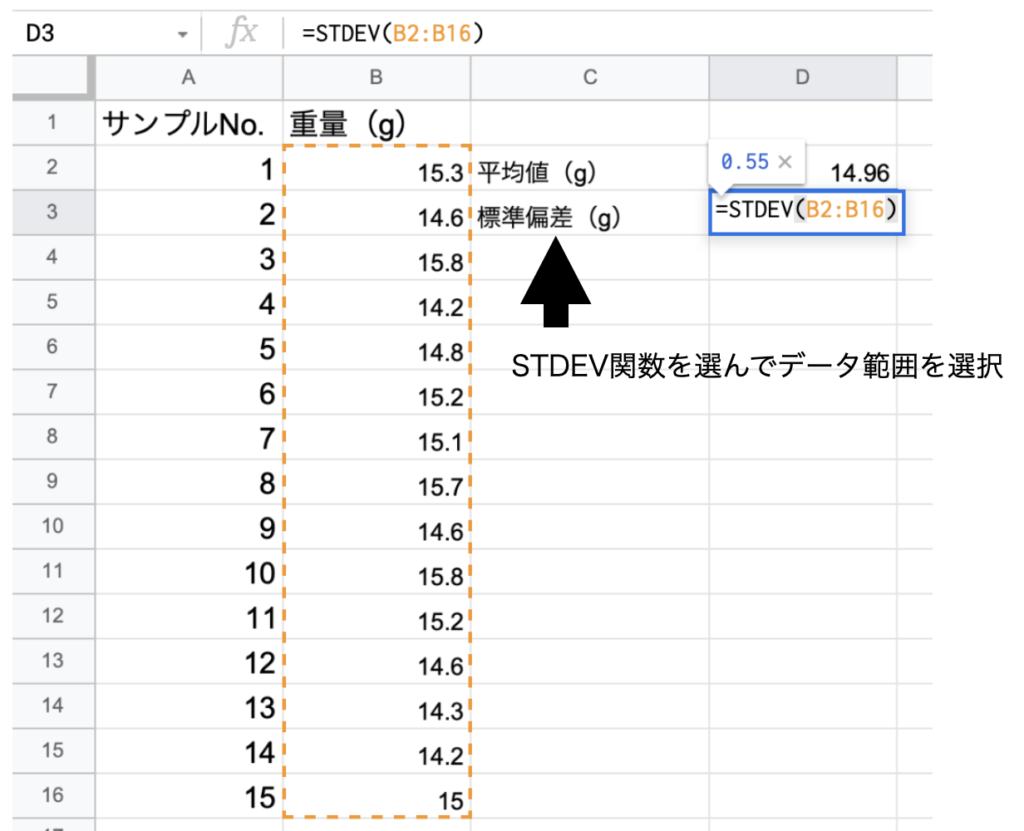
平均値は14.96g、標準偏差は0.55gと出ました。
結論から述べますと、大量に製造したクッキーの重量は以下の範囲に収まる可能性が高いです。

上記のように取得したデータに外れ値(突出して大きいまたは小さい値)がなければ、平均値と標準偏差を使って全体のデータが取り得る値の範囲を推測することができます。
この操作を専門用語で言うと、”母集団の信頼区間を推定する”と表現します。
少ないサンプルから全体の傾向を推測するときの注意点
先ほど平均と標準偏差を使って少ないサンプルから全体のブレ幅を推測しましたが、注意点があります。
かなり厳密さを求めるのであれば、クッキー重量の分布が本当に正規分布に従っているか?とか、正規分布よりt分布に従うのでは?などの検証が必要です。
ただビジネスに応用するレベルなら、外れ値に注意していれば先ほどの考え方で問題ないです。
少ないサンプル数から全体の重量のブレ幅を推測する方法をより詳しく知りたい方はこちらのサイトがおすすめです。
やや専門用語が多いですが、図でブレ幅を表現していてわかりやすいです。
最後に
今回は少ないサンプルデータから全体の傾向を推測する方法について紹介しました。
全数検査が時間的にもお金的にも難しい場合に活用できる強力な推測方法です。
ぜひビジネスなどで活用して下さると嬉しいです。
以上です。最後までお付き合いくださりありがとうございました。

