こんにちは、おちです。
先日平均の考え方と落とし穴についてご紹介しましたが、今回はばらつきの指標である標準偏差についてお話ししていきます。
平均と比べると馴染みがないかもしれませんが、平均同様、標準偏差はデータの全体の特徴や傾向の把握に便利なツールのひとつです。
数式を使った説明は専門書や他のサイトにお任せして、本ブログでは標準偏差の役割や使用時の注意点についてご紹介していきます。
標準偏差も数字に踊らされないよう予め図におこしてデータ全体を俯瞰して見ることが大事です。後ほど詳しくお話しします。
標準偏差とは?〜データのばらつきを表す指標〜
標準偏差はデータのばらつき具合を表す指標のひとつです。
具体的に見てみましょう。平均体重55kgのある2つのグループからランダムにそれぞれ4人選んでグループ全体の傾向を掴もうとした例を見てみます。


どちらのグループも平均体重は55kgですが、一人ひとりを見てみると上のグループの方が痩せている方とふくよかな方がいらっしゃって、下のグループよりも平均値から離れている人が多くばらつきが大きいことがわかりました。
このばらつきの大小を数字で表せるようにした指標が標準偏差です。
2つのグループのばらつきの大きさをそれぞれ標準偏差で表現すると以下のようになります。


標準偏差を使ってばらつきの大きさを数値化することで、どれくらいばらつきの大きさに差があるのかが見えやすくなります。
標準偏差を使う上での注意点〜データを散布図におこそう〜
先ほどの図で紹介したように、標準偏差はデータのばらつきの大きさの程度を推し量るのに便利です。
しかし、平均同様扱いには注意が必要です。平均からあまりにも離れている少数派に引っ張られてデータ全体の特徴・傾向を見誤る可能性があるためです。具体的に見てみましょう。
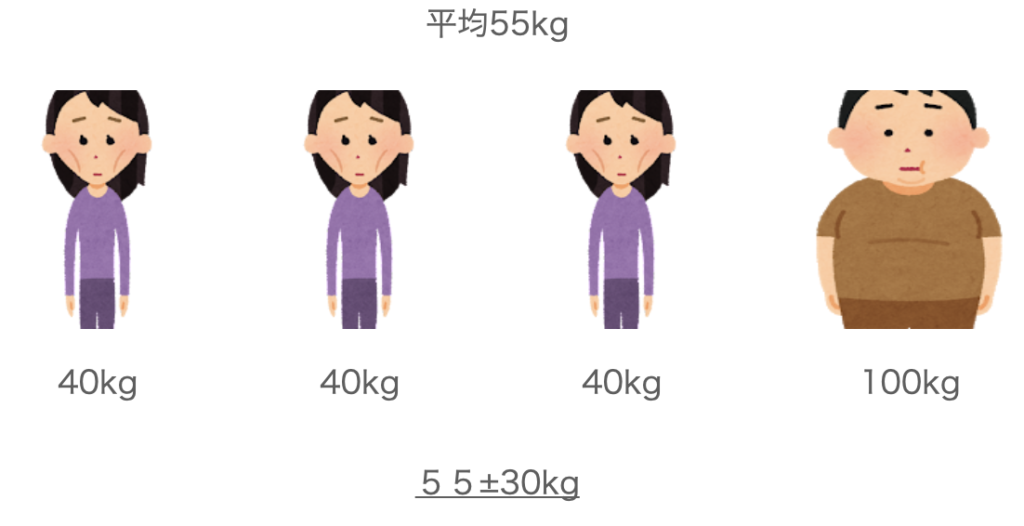

あるグループからランダムに4人選んで体重の平均と標準偏差を見てみると、平均は55kgで標準偏差は30kgでした。
平均と標準偏差だけを見たらものすごくばらつきがあるグループだと思ってしまいそうですが、一人ひとりの体重を見ると、一人だけ他の方よりも体重が重いことがわかります。
再度ランダムに4人選んだら、このグループの平均体重は40kgでばらつきもほどんどないグループという結果が出るかもしれません。
この他の人たちの平均よりも大きく離れた人がいる可能性に注意が必要です。
専門用語でこのような平均から大きく外れたものの値を外れ値と言います。
この外れ値の存在の有無を確認し、データ全体の特徴・傾向を見誤らないためにデータを図におこすことがとても大事になります。
平均同様、まずデータを散布図におこすくせをつけておくと安心です。
最後に
今回はばらつきの指標である標準偏差についてご紹介しました。
平均も標準偏差も大変便利な指標ではあるのですが、安易に使ってしまうとデータ全体の特徴・傾向を見落とす・見誤ることがあります。
使う際は落とし穴に注意して活用していただけたら嬉しく思います。
以上です。最後までお付き合いくださりありがとうございました。

