平均値の落とし穴とその対策をわかりやすく解説してみた

こんにちは、おちです。

今回の記事では平均値の考え方と扱う時にハマりやすい落とし穴についてお話ししていきます。

統計の中では馴染みのある数値な分、落とし穴にハマってデータの結果を読み違えることもあるので注意です。

平均とは？〜なぜ平均を求めることが多いのか？〜

平均の説明は上の通りなのですが、そもそもなぜ平均を求める場面が多いのかをお話しします。

平均値を求める場面が多いのは、見たい対象の全体の傾向を掴むのに便利なことが多いためためです。

例えば全国の男女の身長はどれくらいかを知りたいとします。

パッとしたイメージだと男性は女性よりは身長が高そうと感じるかもしれませんが、一人ひとりを見ると身長150cmの男女も180cmの男女もいます。

一口に全国の男女の身長といっても一人ひとりばらつきが見られます。だから、「身長なんて人それぞれだよね」というのも一つの回答です。

ですが、例えば男性用・女性用のシャツを作って売りたいというときに一人ひとりの身長に合わせて作るのは大変です。

ここで平均値の登場です。多くの男女の方に当てはまりやいシャツの大きさを身長の平均値から予想して量産することができるのです。

平均の落とし穴〜少数派の存在を見落としてしまいがち〜

先程の身長の例で言うと、シャツを作る側からすれば多くの方に合うシャツを効率よく量産できるため便利です。

一方で、平均値から大きく外れた方には合わないシャツばかりが世にある状態になってしまいがちです。

少数派の存在を安易に切り捨ててしまわないよう気を払う必要があります。

逆に少数派に引っ張られて見たい対象全体の傾向を見誤ることがあります。下図をご覧ください。

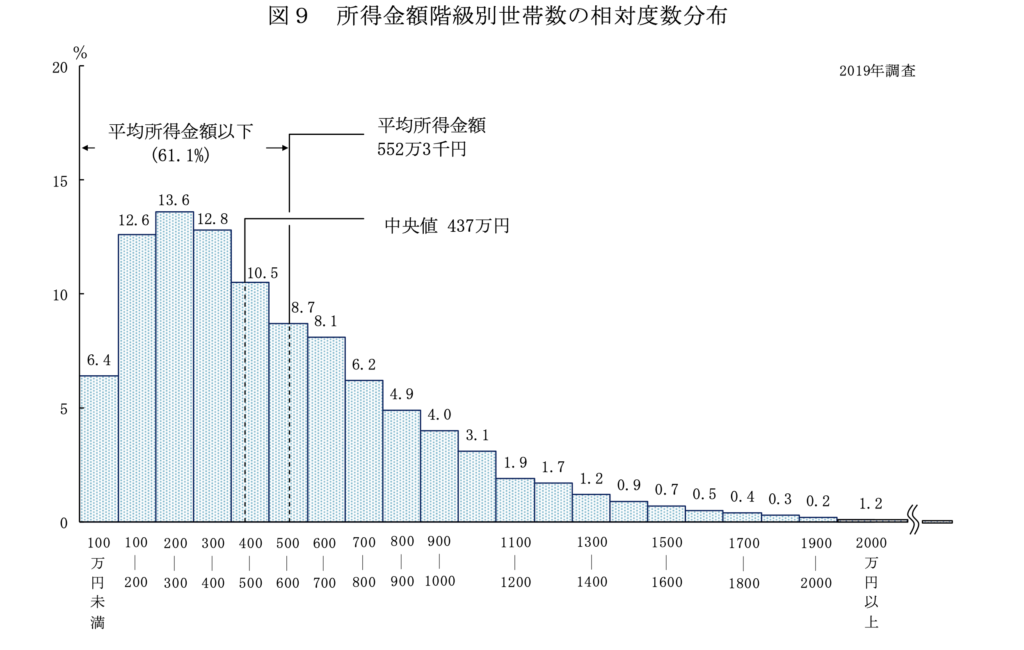
これは年収別の世帯数の分布を表しています。

分布的には年収100〜400万円の世帯が多いにも関わらず、平均年収が552万３千円になっています。

これは高年収の方々の年収が高すぎて平均値を押し上げてしまったためです。

一般的な年収額を知りたいときに平均値を見てしまうと、一般的な世帯年収より高い値となるため、全体の傾向を見誤ってしまいます。

別の記事で紹介しますが、上図のように分布が左右どちらかに偏っている場合は、中央値と呼ばれる値が全体の傾向を把握するのに便利な数字となります。

落とし穴にはまらないために〜データを散布図におこそう〜

普段何気なく使っている平均の落とし穴をご紹介してきました。

この落とし穴にはまらないためにデータを散布図におこすことをお勧めします。

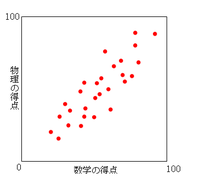
散布図とは上図のように一つひとつのデータを点として図に打ったものです。

散布図は慣れればエクセルで簡単に作れます。平均値を機械的にエクセルで出す前に是非データを散布図におこしてみてください。

散布図を作ると、見たい対象全体の傾向が一目でわかり大変便利です。

少数派が平均と比べてどれだけ外れた位置にいるのかも一目でわかります。また、本当に大部分のデータが平均の近くにいるのかも確認できます。

データをエクセルに入力し終わったら、まず散布図を作るくせをつけると、データの特徴・傾向を見落とす、見誤る機会が減るのでお勧めです。

最後に

平均とその落とし穴についてお話ししました。

統計の中では馴染みのある平均ですが、中々奥が深いことを感じていただけましたら嬉しいです。

以上です。最後までお付き合いくださりありがとうございました。